Black Hole Physics in Interstellar

Introduction

A rotating black hole is needed to replicate the effects in the movie. Here we use the Kerr metric for the spinning black hole:

\[ds^{2}=-\left(1-\dfrac{2 M r}{\rho^{2}}\right)dt^{2}-\dfrac{4 M a r \sin^{2}\theta}{\rho^{2}}d\phi dt+ \dfrac{\rho^{2}}{\Delta}dr^{2}+\rho^{2}d\theta^{2}+\left(r^{2}+a^{2}+\dfrac{2M r a^{2}\sin^{2}\theta}{\rho^{2}} \right)d\phi^{2}, \]

where \(a\equiv J/M\), \(\rho^{2}\equiv r^{2}+a\cos^{2}\theta\), \(\Delta \equiv r^{2}-2M r+a^{2}.\)

In this post, I set \(c=G=1\) unless otherwise specified. One needs to restore \(c\) and \(G\) factors in the results to obtain values in the standard units, for example, \(r=M\) means \(r=MG/c^2.\) For detailed discussion please see reference [1].

Spinning Rate of the Black Hole

[Derived from Time Dilation Factor at the Innermost Stable Circular Orbit (ISCO)]

In the movie, 1 hour on Miller’s planet equals 7 years on earth. To get that time dilation effect, one normally needs to be close enough to the black hole. And because Miller’s planet is in a stable orbit as suggested in the movie, there’s a limit to how close it can be to the black hole. Another way to generate time dilation effects is through the spinning of the black hole. In the following calculation, we will show that to get the time dilation at the innermost stable circular orbit, the black hole needs to spin super fast.

We assume that Miller’s planet is orbiting in the equatorial plane \((\theta=\pi/2)\), so that \(\rho\rightarrow r\), \(\sin\theta\rightarrow1\), \(\cos\theta\rightarrow0,\) and the metric becomes

\[ds^{2}=-\left(1-\dfrac{2 M r}{r^{2}}\right)dt^{2}-\dfrac{4 M a }{r}d\phi dt+ \dfrac{r^{2}}{\Delta}dr^{2}+\rho^{2}d\theta^{2}+\left( r^{2}+a^{2}+\dfrac{2M a^{2}}{r} \right)d\phi^{2}.\]

The horizon is at [2]

\[r_{hr}=M+ \sqrt{M^{2}-a^{2}}.\]

The time dilation for a stable circular orbit is [2]

\[\dfrac{dt}{d\tau}=\dfrac{a \sqrt{M}+r^{3/2}}{\sqrt{2 a \sqrt{M} r^{3/2}-3 M r^2+r^3}}.\]

And the innermost stable circular orbit (ISCO) is at \(r=r_{ISCO}\) which is a solution to the following equation [2]

\[0=1-6\dfrac{M}{r}+8\dfrac{a M^{1/2}}{r^{3/2}}-3\dfrac{a^{2}}{r^{2}}.\]

Plotting \(r_{rh}, r_{ISCO}\) and \(\dfrac{dt}{d\tau}\) as functions of \(r\) and \(a\), we get

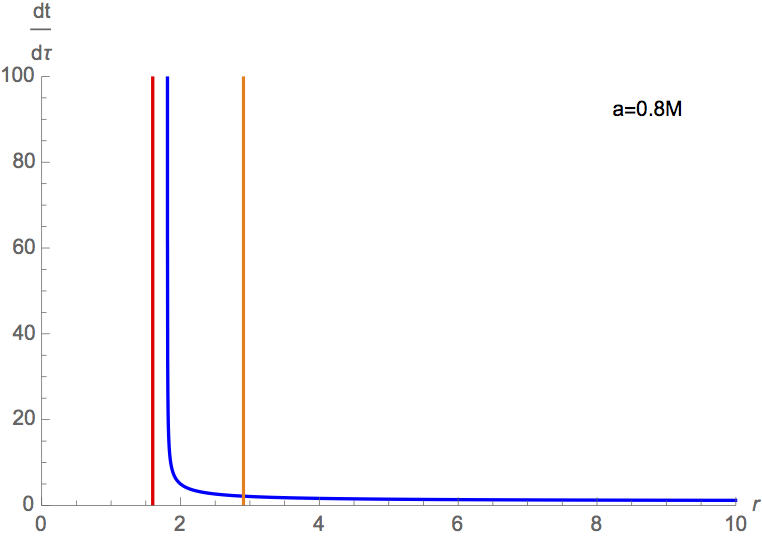
The red line indicates the location of the black hole horizon, the orange line indicates the location of the ISCO, and the blue curve gives the time dilation factor as a function of coordinate \(r\). This plot is generated for \(a=0.8M\). As \(a\) increases, ISCO moves closer to the horizon, and the time dilation at ISCO becomes bigger. Therefore, to get the extreme time dilation of 1 hour equals 7 years as depicted in the movie, the black hole has to spin very fast, and \(a\) takes almost its extremal value \(M.\) We now proceed to derive this spin rate.

We parametrize \(a\) in the following way:

\[a=M(1-\epsilon), \] where \(\epsilon\) is very small. With the equations quoted above, it follows that [2]

\[r_{hr}=M(1+\sqrt{2\epsilon}), \]

\[r_{ISCO}=M[1+(4\epsilon)^{1/3}].\]

The time dilation at this \(r_{ISCO}\) is therefore

\[\left.\dfrac{dt}{d\tau}\right|_{ISCO}=\dfrac{2}{\sqrt{3}}\left(\dfrac{2}{\epsilon}\right)^{1/3}.\]

Setting it to \(\dfrac{\text{7 years}}{\text{1 hour}}=61320,\) we find \(\epsilon=1.34 e -14.\)

Assuming Miller’s planet is at this innermost stable circular orbit, then this is the appropriate \(\epsilon\) value for the movie. Therefore the black hole in the movie is spinning at a rate that’s only 100 trillionths away from the maximum. And the horizon and innermost stable orbit are at \(r_{hr}=1.00000016M,\) and \(r_{ISCO}=1.00004M.\)

Mass of the Black Hole

[Derived From Tidal Force Balance]

The tidal force generated by the black hole across Miller’s planet must be smaller than the inward gravitational acceleration on the planet’s surface generated by the planet’s mass, otherwise, the planet would be torn apart. Using this fact, we can derive the limit to the mass of the black hole.

First, let’s derive the tidal force generated across Miller’s planet. Two conserved quantities can be found respectively, because the metric has a time translation symmetry under \(t\rightarrow t+\delta t\) and azimuthal symmetry under \(\phi\rightarrow \phi+\delta\phi\) (see [1, 2] and [here]):

\[e=\dfrac{1 - 2M/r + a M^{1/2}/r^{3/2}}{\sqrt{1 - 3M/r + 2 a M^{1/2}/r^{3/2}}},\]

\[l=\dfrac{M^{1/2}r^{1/2}-2 a M/r + M^{1/2}a^{2}/r^{3/2}}{\sqrt{1 - 3M/r + 2aM^{1/2}/r^{3/2}}}.\]

Plugging in the \(r_{ISCO}\) and \(a\) values derived for this movie, one gets

\[e=0.57737,\]

\[l=1.15474M,\]

for the innermost stable circular orbit.

The radial velocity at \(r\) is given by [1]

\[\dfrac{dr}{d\tau}=\sqrt{e^2-1+\dfrac{2 M}{r}-\dfrac{l^2-a^2 \left(e^2-1\right)}{2 r^2}+\dfrac{2 M (l-a e)^2}{r^3}}.\]

The gravitational acceleration is obtained by

\[g=\dfrac{d^{2}r}{d\tau^{2}}=\dfrac{d^{2}r}{d\tau dr}\dfrac{dr}{d\tau}, \]

so the gravitational difference across the radius of Miller’s planet \(r_{Miller}\) in the radial direction is

\[g_{tidal}=\dfrac{dg}{dr}r_{Miller}=\dfrac{3c^{6}}{M^{2}G^{2}}r_{Miller}, \]

where c and G are restored in the last step and \(r_{ISCO}=1.00004M\) is used. Notice that this differs from Kip Thorne’s formula because he used the familiar Newtonian gravitational acceleration generated by a mass at rest (\(GM/R^2\)), which gives the tidal force

\[g_{tidal}=\dfrac{2 G M}{R^{3}}r_{Miller}=\dfrac{2c^{6}}{M^{2}G^{2}}r_{Miller}, \]

where \(R=r_{ISCO}\simeq M\) is used and c and G restored in the last step. Also, notice that because we assume the

On the other hand, the gravitational acceleration produced by Miller’s planet on the surface is

\[g_{Miller}=G\dfrac{\dfrac{4\pi}{3}r^{3}\rho}{r^{2}}=\dfrac{4\pi}{3}G r\rho.\]

The condition that tidal force does not rip apart Miller’s planet is

\[g_{Miller}>g_{tidal}.\]

With \(\rho=10000\; kg/m^{3}\) (number chosen by Kip Thorne for that of compressed rock), our tidal force would give

\[M_{bh}>\dfrac{3 c^{3}}{\sqrt{4\pi G^{3}\rho}}=4.2e38\; kg\]

or about the same as 210 million suns, while Kip Thorne’s tidal acceleration would result in

\[M_{bh}>\dfrac{\sqrt{3}c^{3}}{\sqrt{2\pi G^{3}\rho}}=3.4e38\; kg\]

or about the same as 170 million suns.

Kip Thorne chose the mass of the black hole to be about 100 million suns as an approximation in his book, acknowledging that it should be 200 million suns. So for the sake of comparison, we will also use \(M_{bh}=1e8 M_{sun}=1.99e38\; kg\) from now on.

For later convenience, we here define a distance unit corresponding to this black hole mass:

\[r_{unit}=\dfrac{M_{bh} G}{c^{2}}=1.47e8\; km, \] which is about the same as the earth-sun distance.

Position of Miller’s Planet and the Parking Orbit

To get a sense of relative scale, we can ask: what are the radial distances of Miller’s planet and the parking orbit to the event horizon of the black hole?

Chris Nolan wanted the parking orbit to have modest time dilation relative to the earth, so in Kip’s interpretation, he chose the parking orbit at \(r_{parking}=10M_{bh}=10r_{unit}.\) Plugging this value into the \(dt/d\tau\), we find the time dilation factor at this orbit to be about 1.2 (compared to earth time), which is reasonable.

Note that because of the distortion in space, the circumference of the orbit is much less than \(2\pi\) times the radial proper distance to the center of the black hole (the distance traveling on the membrane in the following figure). We reduce the 3-dimensional space to 2-dimension, and use the third direction to show what our space looked like in a higher dimension:

The yellow circle is the parking orbit for Endurance, the blue circle is the orbit for Miller’s planet, and the black circle at the bottom is the horizon. We see that because of the space distortion, even though the \(r_{ISCO}\) value is very close to \(r_{hr}\) (which produces similar radii for the circles), the proper distance between them (the distance on this “membrane” traversed by the spaceship) is much larger than expected.

The radius of the circle is the proper distance of the orbit divided by \(2\pi\), and is given by \(g_{\phi\phi}\) of the metric \(R=\sqrt{\frac{2 a^2 M}{r}+a^2+r^2}\). Note that \(R>r\) due to the spinning of the black hole (\(a\neq0\)). For the parking orbit, \(R_{parking}\approx10M_{bh}\approx10r_{unit}\), the same as the coordinate \(r\). For Miller’s planet and the horizon, \(R_{ISCO}\approx R_{hr}=2M_{bh}=2r_{unit}\), twice the coordinate \(r_{ISCO}\) and \(r_{hr}.\)

We now wish to calculate the proper distance between \(r_{ISCO}\) and \(r_{hr}\), and the proper distance between \(r_{ISCO}\) and \(r_{parking}\). From the metric, we have

\[\dfrac{ds}{dr}=\sqrt{\dfrac{r^2}{a^2-2 M r+r^2}}.\]

We use the parametrization of \(r_{ISCO}=M_{bh}(1+\xi_{ISCO})\), \(r_{hr}=M_{bh}(1+\xi_{hr})\) and \(a=M_{bh}(1-\epsilon)\). The integration produces

\[\int_{M_{bh}(1+\xi_{ISCO})}^{M_{bh}(1+\xi_{hr})}\dfrac{ds}{dr}dr=M_{bh}\log\left[\dfrac{\xi_{ISCO} +\sqrt{\xi_{ISCO} ^2+\epsilon ^2-2 \epsilon}}{\xi_{hr} +\sqrt{\xi_{hr} ^2+\epsilon ^2-2 \epsilon}}\right]\simeq6.1M_{bh}=6.1r_{s}, \]

or 6.1 times the earth-sun distance. Direct numerical integration for the proper distance between \(r_{ISCO}\) and \(r_{parking}\) gives 21.4 times the earth-sun distance.

Orbital Periods at \(r_{ISCO}\) and \(r_{parking}\)

The angular velocity is given by [2]

\[\omega=\dfrac{d\phi}{dt}=\dfrac{\sqrt{M}}{a \sqrt{M}+r^{3/2}}\dfrac{c^{3}}{G}, \]

where c and G are restored.

We immediately obtain \(\omega_{ISCO}=0.001\; s^{-1}\) and \(\omega_{parking}=0.000062\; s^{-1}\), corresponding to 1.7 hours for Miller’s planet and 28 hours for the parking orbit respectively. Because the time slows down a factor of 61320 on Miller’s planet, the 1.7 hour period measured on the planet would be only 0.1 second, which means the planet travels around this \(2\pi R_{ISCO}=8\pi r_{unit}\) circumference 10 times per second! That seems super fast! In fact, it’s faster than the speed of light! How can that be? Well, as Kip explains in his book, because of the space whirl induced by the black hole’s fast spin, this is slower than the local speed of light, and because of the free-falling motion, the centripetal force felt by the planet is negligible compared to the more important tidal force.

Rocking Period of Miller’s Planet Induced by the Tidal Force

In one of Kip’s interpretations, the waves are possibly created by the rocking of the planet under the tidal force of the black hole. As he explained in his book, the planet has its face almost locked to the black hole, because otherwise the mantle would be pulverized under the tidal force. But, to produce the huge waves seen in the movie, the planet needs to rock back and forth a bit.

I now attempt to calculate the period of this rocking motion in a very simplified model.

Under the tidal force, Miller’s planet would be stretched and squeezed to an ellipsoid shape. The red lines indicate the stretching direction and the blue lines indicate the squeezing direction. Let’s say the planet’s semi-major axis has length \(l,\) then the torque produced by each half hemisphere has the lever arm distance of \(l/2\theta.\) So the torque produced by the tidal force in the black hole radial direction can be approximated to be \(-\dfrac{m}{2}g_{tidal}\dfrac{l}{2}\theta\), where \(m/2\) is the mass of each hemisphere.

There is another torque produced by the squeezing force in the orbital direction (see Kip Thorne’s book), but here instead of calculating that, we take a guess, and approximate it to be the same amount as the torque above. Therefore, the total torque is \(-\dfrac{m}{2}g_{tidal}l\theta.\) To simplify the problem further, we use the moment of inertia formula for a solid ball instead of an ellipsoid and approximate \(r_{miller}\approx l\), i.e. \(I=\dfrac{2}{5}m l^{2}.\) We then have

\[\dfrac{2}{5}m l^{2}\dfrac{d^{2}\theta}{dt^{2}}+\dfrac{m}{2}g_{tidal}l\theta=0.\]

The period of the oscillation is

\[\omega=\sqrt{\dfrac{5}{4}\dfrac{c^{6}}{G^{2}M}}, \]

where c and G are restored. Plugging in \(M=M_{bh}\), this gives 0.0023 per second, or a period of 27 minutes, about half an hour. This differs from Kip’s result of 1 hour, which is also the time between waves used in the movie. But considering the estimation I did was quite poor, I’m happy with the result.

References

[1] J. B. Hartle, Gravity: An Introduction to Einstein’s General Relativity (Benjamin Cummings, 2003).

[2] S. Chandrasekhar, The Mathematical Theory of Black Holes (Clarendon Press, Oxford University Press).